什么是线段树

前言

本文主要从三个方面来讲述线段树 (segment tree) 是什么. 即, 线段树的特性, 线段树的实现方式, 以及线段树可以解决什么问题这三个方面. 另, 本文主要参考了 oi-wiki1.

线段树的性质

线段树可以在 \(O(\log N)\) 的时间复杂度内实现单点修改、区间修改、区间查询（区间求和，求区间最大值，求区间最小值）等操作。

如何实现一个线段树

设有一大小为 \(5\) 的数组 \(a=\{10,11,12,13,14\}\) 其所转化为的线段树如下图

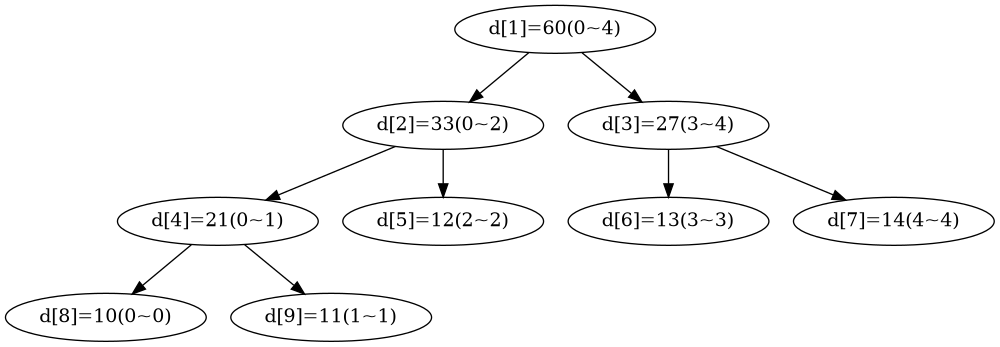
其中, 线段树 \(d\) 的每个节点代表 \((a, b)\) 范围内的 \(a\) 每个元素的和. 如果以递归的方式实现线段树的话会比较简单, 如下, 代码参考 oi-wiki

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11

void build(int s, int t, int p) {
  // 对 [s,t] 区间建立线段树,当前根的编号为 p
  if (s == t) {
    d[p] = a[s];
    return;
  }
  int m = (s + t) / 2;
  build(s, m, p * 2), build(m + 1, t, p * 2 + 1);
  // 递归对左右区间建树
  d[p] = d[p * 2] + d[(p * 2) + 1];
}

这里使用的是堆式存储, 即对数组下标 \(i\) , 右孩子的下标是 \(i\times2+1\), 左孩子的下标是 \(i\times2\). 特别的, 如果 \(d[i]\) 表示的是区间 \([s,t]\) 的话, 那么 \(d[i]\) 的左儿子节点表示的区间是 \([s, \frac{s+t}{2}]\), \(d[i]\) 的右孩子表示的是区间 \([\frac{s+t}{2}+1, t]\)

线段树的区间查询

一般的, 如果要查询区间, \([l,r]\) 则可以将其拆成最多为 \(O(\log n)\) 个极大的区间, 合并这些区间即可求出 \([l,r]\) 的答案. 代码如下

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11

int getsum(int l, int r, int s, int t, int p) {
  // [l,r] 为查询区间,[s,t] 为当前节点包含的区间,p 为当前节点的编号
  if (l <= s && t <= r)
    return d[p];  // 当前区间为询问区间的子集时直接返回当前区间的和
  int m = (s + t) / 2, sum = 0;
  if (l <= m) sum += getsum(l, r, s, m, p * 2);
  // 如果左儿子代表的区间 [l,m] 与询问区间有交集,则递归查询左儿子
  if (r > m) sum += getsum(l, r, m + 1, t, p * 2 + 1);
  // 如果右儿子代表的区间 [m+1,r] 与询问区间有交集,则递归查询右儿子
  return sum;
}

线段树的区间修改与惰性标记

当修改了 \([l,r]\) 中的至少一个元素时, 需要把所有包含了 \([l,r]\) 中的节点的线段树节点进行更新, 时间复杂度太大, 难以承受. 这里可以使用惰性标记来优化时间复杂度. 设置一个数组 \(b\), 其中 \(b[i]\) 为 \(d[i]\) 的惰性标记. 当要查询时就把惰性标记向下传递 区间修改(区间加上某个值)

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18

void update(int l, int r, int c, int s, int t, int p) {
  // [l,r] 为修改区间,c 为被修改的元素的变化量,[s,t] 为当前节点包含的区间,p
  // 为当前节点的编号
  if (l <= s && t <= r) {
    d[p] += (t - s + 1) * c, b[p] += c;
    return;
  }  // 当前区间为修改区间的子集时直接修改当前节点的值,然后打标记,结束修改
  int m = (s + t) / 2;
  if (b[p] && s != t) {
    // 如果当前节点的懒标记非空,则更新当前节点两个子节点的值和懒标记值
    d[p * 2] += b[p] * (m - s + 1), d[p * 2 + 1] += b[p] * (t - m);
    b[p * 2] += b[p], b[p * 2 + 1] += b[p];  // 将标记下传给子节点
    b[p] = 0;                                // 清空当前节点的标记
  }
  if (l <= m) update(l, r, c, s, m, p * 2);
  if (r > m) update(l, r, c, m + 1, t, p * 2 + 1);
  d[p] = d[p * 2] + d[p * 2 + 1];
}

区间查询(区间求和)

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17

int getsum(int l, int r, int s, int t, int p) {
  // [l,r] 为修改区间,c 为被修改的元素的变化量,[s,t] 为当前节点包含的区间,p
  // 为当前节点的编号
  if (l <= s && t <= r) return d[p];
  // 当前区间为询问区间的子集时直接返回当前区间的和
  int m = (s + t) / 2;
  if (b[p]) {
    // 如果当前节点的懒标记非空,则更新当前节点两个子节点的值和懒标记值
    d[p * 2] += b[p] * (m - s + 1), d[p * 2 + 1] += b[p] * (t - m),
        b[p * 2] += b[p], b[p * 2 + 1] += b[p];  // 将标记下传给子节点
    b[p] = 0;                                    // 清空当前节点的标记
  }
  int sum = 0;
  if (l <= m) sum = getsum(l, r, s, m, p * 2);
  if (r > m) sum += getsum(l, r, m + 1, t, p * 2 + 1);
  return sum;
}

应当在什么时候使用线段树

具体主要应用在对区间进行诸如求和,求最大值,求最小值操作的场景

  1. Sum Of Given Range 2
  2. Range Minimum Query 3
  3. Number of Longest Increasing Subsequence 4

  1. https://oi-wiki.org/ds/seg/ ↩︎

  2. https://www.geeksforgeeks.org/segment-tree-set-1-sum-of-given-range/ ↩︎

  3. https://www.geeksforgeeks.org/segment-tree-set-1-range-minimum-query/ ↩︎

  4. https://leetcode-cn.com/problems/number-of-longest-increasing-subsequence/ ↩︎